有向图的连通性

一、基本概念

强连通：在有向图 $G$ 中，如果两点 $u$ , $v$ 是互相可达的，则称 $u$ 和 $v$ 是强连通的。如果 $G$ 中的任意两个点都是互相可达的，那么 $G$ 就是强连通图。

强连通分量：如果一个有向图 $G$ 不是强连通图，那么可以把它分成多个子图，其中每个子图的内部是强连通的，而且这些子图已经扩展到最大，不能与子图外的任一点强连通，像这样的一个“极大强连通”子图是$G$的一个强连通分量( $\text{Strongly Connected Component}$，$\text{SCC}$ ).

$Tarjan$算法能在一次DFS中吧所有点都按 $\text{SCC}$ 分开。这并不是不可思议的，它利用了 $\text{SCC}$ 的特点。

定理：一个 $\text{SCC}$，从其中任何一个点出发。都至少有一条路径能绕回到自己。

二、算法实现

在讲解之前，先了解$low$和$num$操作。

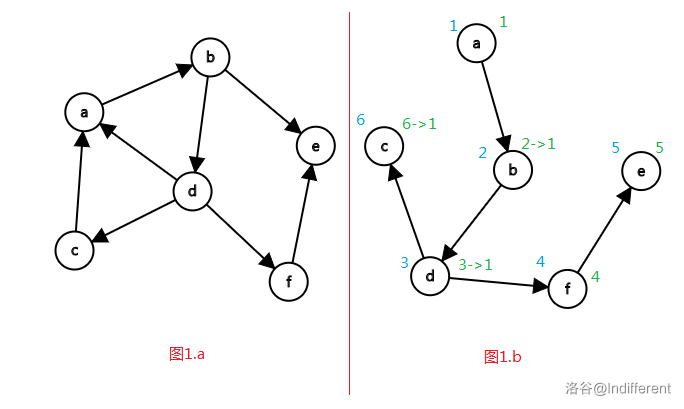
下面是一个例子，下图有三个 $\text{SCC}$，也就是$\{a,b,d,c\}$、$\{e\}$、$\{f\}$.

图1.a是原图。图1.b是对它做$DFS$，每个点左边的数字标记了$DFS$访问它的顺序，也就是$num[]$值，右边的划线数字是$low[]$值，即能返回到的最远的祖先。每个点的$low[]$初始值等于$num[]$，即连到自己。观察$c$的$low[]$值是如何更新的：它的初始值是$6$，然后有一个回退到$a$，所以更新为$1$；它的递归祖先$d$、$b$的$low[]$值也跟着更新为$1$。$e$和$f$的$low[]$值不能更新。

图1.b是从$a$开始$DFS$的，$a$成为{$a,b,d,c$}这个$SCC$的祖先.其实，从{$a,b,d,c$}中任意一个点开始$DFS$，这个点都会成为这个$SCC$的祖先。认识到这些，可以帮助我们理解后面的解释：可以用栈分离不同的$SCC$。

图1.b中的$low[]$值有$3$部分，即等于$1$的{$a,b,d,c$}、等于$4$的{$f$}、等于$5$的{$e$}。这就是$3$个$SCC$。

完成以上步骤，似乎已经就解决了问题。每个点都有了自己的$low[]$值，相同$low[]$值的点属于一个$SCC$。那么只要再对所有点做一个查询，按$low[]$值分开就行了，其复杂度是$O(V)$。

其实有更好的办法，即在$DFS$的同时把点按$SCC$（有相同的$low[]$值）分开。

以图2为例，其中有3个$SCC$，即$A$、$E$、$F$。假设从F中的一个点开始$DFS$，$DFS$过程可能会中途跳出$F$，转入$A$或者$E$，总之，最后会进入一个$SCC$。

假设DFS过程是$F$->$E$->$A$，最后进入$A$。
在$A$这个$SCC$中将完成$A$内所有点的$DFS$过程，也就是说，最后的几步$DFS$会集中在A中的点$a$、$b$、$c$、$d$。这几个点会计算得到相同的$low[]$值，标记为一个$SCC$，这样就好了。
$DFS$递归从$A$回到$E$。并在E中完成$E$内部的$DFS$过程。
回到$F$，在$F$内完成递归过程。

以上过程如何编程？那你可能想起来，$DFS$搜索是用递归实现的，而递归和栈这种数据结构在本质上是一致的。所以，可以用栈来帮助处理。