一、基本概念

欧拉路径：从图中一个结点出发走出一条道路，每条边恰好经过一次的路径。

欧拉回路：从图中任意一个顶点出发走出一条道路，每条边恰好经过一次，并最终回到起点。这样的路径称为“欧拉回路”。（类似于一笔画问题）

欧拉图：具有欧拉回路的图。

半欧拉图：具有欧拉路径但不具有欧拉回路的图

二、算法实现

对于求欧拉回路，我们可以分为两种情况解决：

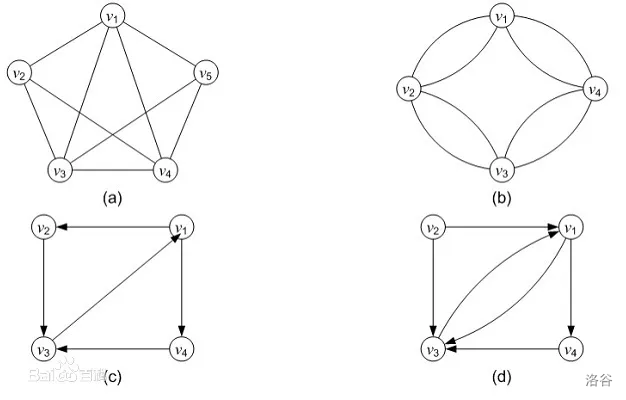
无向图的欧拉回路(图a、b)：对于无向图，只要是一个连通图并且每个点的度是偶数，那么这个图就能构成欧拉回路。
有向图的欧拉回路(图c、d)：对于有向图，只要是一个连通图并且每个点的入度等于出度，那么这个图就能构成欧拉回路。

对于求欧拉路径，我们也可以分为两种情况解决：

无向图的欧拉路径：对于无向图，只有是一个连通图，并且两个点的度为奇数，剩余为偶数是，那么这个图就能有欧拉路径。
有向图的欧拉路径：对于有向图，只要是一个连通图，并且一个点的入度等于出度加一，一个点的入度等于出度减一，其余点入度等于出度时，这个图就有欧拉路径。

一个欧拉图一定有欧拉路径。

2.1 \(\quad\) 无向图的欧拉路径

我们首先判断存在性：

连通；
奇点个数为 \(0\) 或 \(2\)。

通常使用并查集判断连通性，或者走完所有边，判断是否走到了所有的边（这一步在算法流程中进行，否则会破坏时间复杂度）。

考虑如果存在奇点，则路径只能从奇点走若干边（顺序是随意的，不妨自己证明一下）再次到达另一个奇点。

我们找到奇点（或者不存在），然后按边进行 dfs，注意，每条边在欧拉路径中存在且仅存在一次，且顺序随意，所以我们必须标记使用过的边，以避免反复遍历所造成的时间复杂度破坏。我们使用栈记录走过的点，输出时从栈顶以此弹出。

时间复杂度 \(O(m)\)。

void dfs(int u){
	for(int &i=head[u];i;i=nxt[i]){//使用链式前向星存图，注意i变量要取地址，以标记使用过的边，不会再次遍历。
		if(vis[i]) continue;
		int v=to[i];
		vis[i]=vis[i^1]=1;
		dfs(v);
	}
	s[++top]=u;
}

2.2 \(\quad\) 无向图的欧拉回路

和上面类似地，判断存在性：

连通图；
均为偶点。

随意找一个点开始遍历。注意：因为找的是欧拉回路，不必要访问或判断没有边相连的点的连通性。所以，严格地说，找一个有边相连的点开始遍历。

遍历的注意事项和 2.1 大致相同，注意避免重复遍历。唯一不同的是，因为是欧拉回路，会构成一个环，所以，不必要使用栈记录走过的点。当然，这样记录也没有问题。

时间复杂度 \(O(m)\)。

#include<iostream>
using namespace std;
#define MAXN 1000005
int n,m,tot=1,s[MAXN],top,du[MAXN];
int head[MAXN],nxt[MAXN<<1],to[MAXN<<1];
bool vis[MAXN<<1],viss[MAXN];
void dfs(int u){
	for(int &i=head[u];i;i=nxt[i]){
		if(vis[i]) continue;
		int v=to[i];
		vis[i]=vis[i^1]=1;
		dfs(v);
	}
	s[++top]=u;
}
void add(int x,int y){
	to[++tot]=y,nxt[tot]=head[x],head[x]=tot;
	to[++tot]=x,nxt[tot]=head[y],head[y]=tot;
}
int main(){
	ios::sync_with_stdio(0);
	cin>>n>>m;
	for(int x,y,i=1;i<=m;i++){
		cin>>x>>y;
		add(x,y);
		du[x]++,du[y]++;
	}
	for(int i=1;i<=n;i++){
		if(du[i]){
			dfs(i);
			break;
		}
	}
	if(top<=m){
		cout<<-1;
		return 0;
	}
	while(top) cout<<s[top--]<<" ";
	return 0;
}

2.3 \(\quad\) 有向图的欧拉路径

我们首先判断存在性：

连通；
如下两个条件满足其一：
- 所有点入度等于出度；
- “有且仅有一个点出度比入度大一”、“与有且仅有一个点出度比入度小一”两个条件同时成立。

如果满足条件1，随意找点开始遍历（同样抛弃孤立点）；如果满足条件2，找到“出度比入度大一”的点开始遍历，最后一定会回到“出度比入度小一”的点。

按边进行 dfs，详细内容与 2.1类似，可以用邻接表存图。

时间复杂度 \(O(m)\)。

void dfs(int u){
	for(int i=now[u];i<g[u].size();i=now[u]){
		int v=g[u][i];
		now[u]++;
		dfs(v);
	}
	s[++top]=u;
}

2.4 \(\quad\) 有向图的欧拉回路

首先判断存在性：

连通；
每个点的入度等于出度。

随便找一个非孤立点开始遍历，内容同上。

#include<iostream>
#include<vector>
using namespace std;
#define MAXN 1000005
int n,m,in[MAXN],out[MAXN],now[MAXN];
int s[MAXN],top;
vector<int> g[MAXN];
void dfs(int u){
	for(int i=now[u];i<g[u].size();i=now[u]){
		int v=g[u][i];
		now[u]++;
		dfs(v);
	}
	s[++top]=u;
}
int main(){
	cin>>n>>m;
	for(int x,y,i=1;i<=m;i++){
		cin>>x>>y;
		g[x].push_back(y);
		in[y]++;
		out[x]++;
	}
	int st=0,numin=0,numout=0;
	for(int i=1;i<=n;i++){
		if(in[i]!=out[i]){
			cout<<-1;
			return 0;
		}
	}
	if(numin>1||numout>1){
		cout<<-1;
		return 0;
	}
	for(int i=1;i<=n;i++) if(out[i]){
		st=i;
		break;
	}
	dfs(st);
	if(top!=m+1){
		cout<<-1;
		return 0;
	}
	while(top){
		cout<<s[top--]<<" ";
	}
	return 0;
}