线段树
线段树
线段树,OI中重要的数据结构,用于维护区间信息,也可以辅助维护。线段树的性能比树状数组强(但是码量大),普遍复杂度在 $O(\log n)$ 左右。
一、基本概念
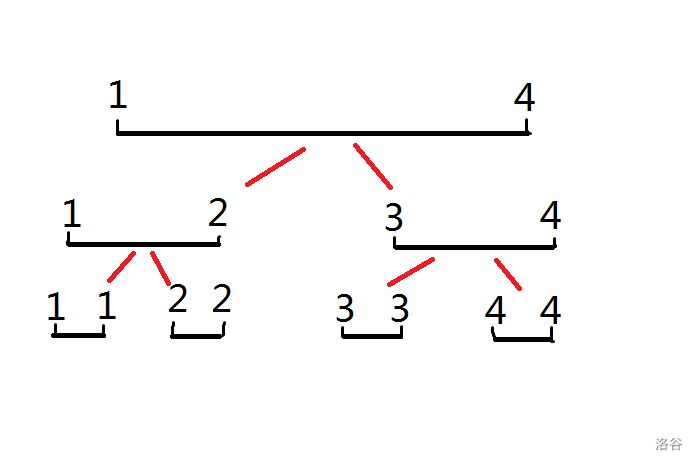
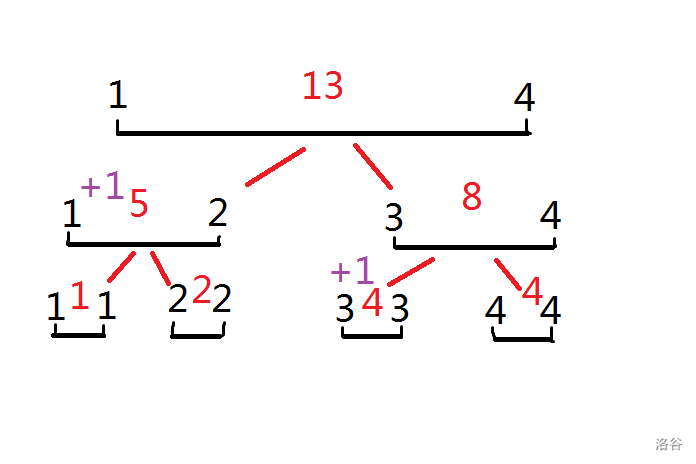
线段树是一种二叉树,也就是对于一个线段,我们会用一个二叉树来表示。比如说一个长度为4的线段,我们可以表示成这样:
这是什么意思呢? 如果你要表示线段的和,那么最上面的根节点的权值表示的是这个线段 $1\sim 4$ 的和。根的两个儿子分别表示这个线段中 $1\sim 2$ 的和,与 $3\sim 4$ 的和。以此类推。
然后我们还可以的到一个性质:节点i的权值=她的左儿子权值+她的右儿子权值。因为 $1\sim 4$ 的和就是等于 $1\sim 2$ 的和加上 $3\sim 4$ 的和。
根据这个思路,我们就可以建树了,我们设一个结构体 tree,tree[i].l 和 tree[i].r 分别表示这个点代表的线段的左右下标, tree[i].sum 表示这个节点表示的线段和。
我们知道,一颗二叉树,她的左儿子和右儿子编号分别是 $p\times2$ 和 $p\times2+1$。
再根据刚才的性质,得到式子:tree[i].sum=tree[i*2].sum+tree[i*2+1].sum 就可以建一颗线段树了!
代码如下:1
2
3
4
5
6
7
8
9
10
11inline void build(int i,int l,int r){//递归建树
tree[i].l=l;tree[i].r=r;
if(l==r){//如果这个节点是叶子节点
tree[i].sum=input[l];
return ;
}
int mid=(l+r)>>1;
build(i*2,l,mid);//分别构造左子树和右子树
build(i*2+1,mid+1,r);
tree[i].sum=tree[i*2].sum+tree[i*2+1].sum;//刚才我们发现的性质return ;
}
嗯,这就是线段树的构建,你可能会问为什么要开好几倍的内存去储存一条线段。这是因为我们还没有让这个过大的数组干一些实事,那么什么是实事呢?让我们进入下一部(在你看懂这一部的情况下)
二、简单的线段树
2.1$\quad$单点修改,区间查询
其实这一章开始才是真正的线段树,我们要用线段树干什么?答案是维护一个线段(或者区间),比如你想求出一个 $1\sim 100$ 区间中, $4\sim 67$ 这些元素的和,你会怎么做?朴素的做法是 for(i=4;i<=67;i++) sum+=a[i],这样固然好,但是算得太慢了。
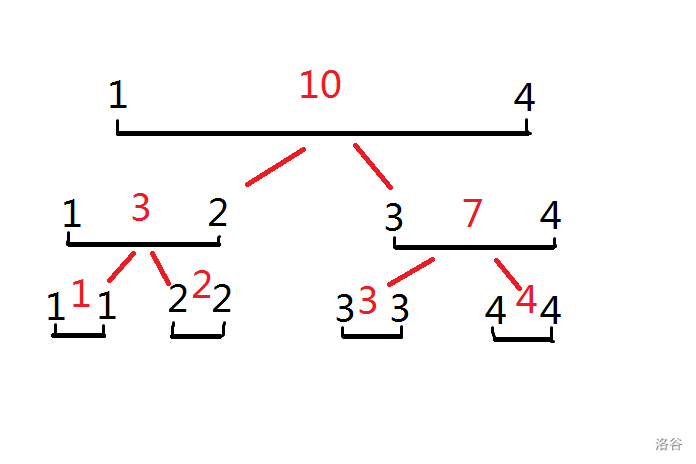
我们想一种新的方法,先想一个比较好画图的数据,比如一个长度为4的区间,分别是1、2、3、4,我们想求出第 $1\sim 3$ 项的和。按照上一部说的,我们要建出一颗线段树,其中点权(也就是红色)表示和:
然后我们要求 $1\sim 3$ 的和,我们先从根节点开始查询,发现她的左儿子 $1\sim 2$ 这个区间和答案区间 $1\sim 3$ 有交集,那么我们跑到左儿子这个区间。
然后,我们发现这个区间 $1\sim 2$ 被完全包括在答案区间 $1\sim 3$ 这个区间里面,那就把她的值3返回。
我们回到了 $1\sim 4$ 区间,发现她的右儿子 $3\sim 4$ 区间和答案区间 $1\sim 3$ 有交集,那么我们走到 $3\sim 4$ 区间
到了 $3\sim 4$ 区间,我们发现她并没有完全包含在答案区间 $1\sim 3$ 里面,但发现她的左儿子 $3\sim 3$ 区间和 $1\sim 3$ 区间又交集,那么久走到 $3\sim 3$ 区间
到了 $3\sim 3$ 区间,发现其被答案区间完全包含,就返回她的值3一直到最开始
$3\sim 32$ 区间的 $3+1\sim 2$ 区间的3=6,我们知道了 $1\sim 3$ 区间和为6。
我们总结一下,线段树的查询方法:
- 如果这个区间被完全包括在目标区间里面,直接返回这个区间的值
- 如果这个区间的左儿子和目标区间有交集,那么搜索左儿子
- 如果这个区间的右儿子和目标区间有交集,那么搜索右儿子
写成代码,就会变成这样:1
2
3
4
5
6
7
8
9inline int search(int i,int l,int r){
if(tree[i].l>=l && tree[i].r<=r)//如果这个区间被完全包括在目标区间里面,直接返回这个区间的值
return tree[i].sum;
if(tree[i].r<l || tree[i].l>r) return 0;//如果这个区间和目标区间毫不相干,返回0
int s=0;
if(tree[i*2].r>=l) s+=search(i*2,l,r);//如果这个区间的左儿子和目标区间又交集,那么搜索左儿子
if(tree[i*2+1].l<=r) s+=search(i*2+1,l,r);//如果这个区间的右儿子和目标区间又交集,那么搜索右儿子
return s;
}
关于那几个if的条件一定要看清楚,最好背下来,以防考场上脑抽推错。
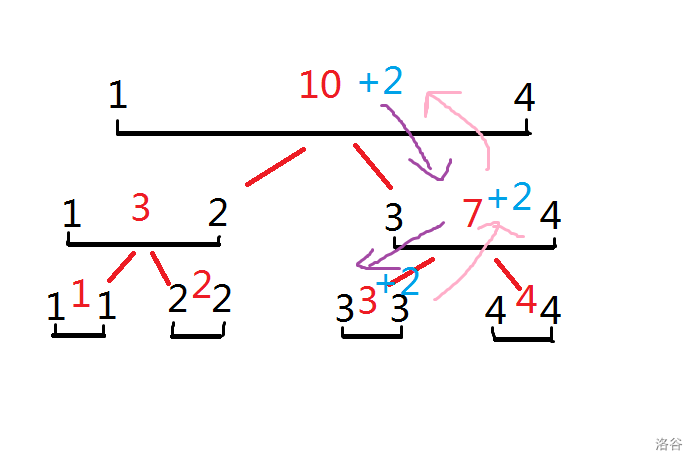
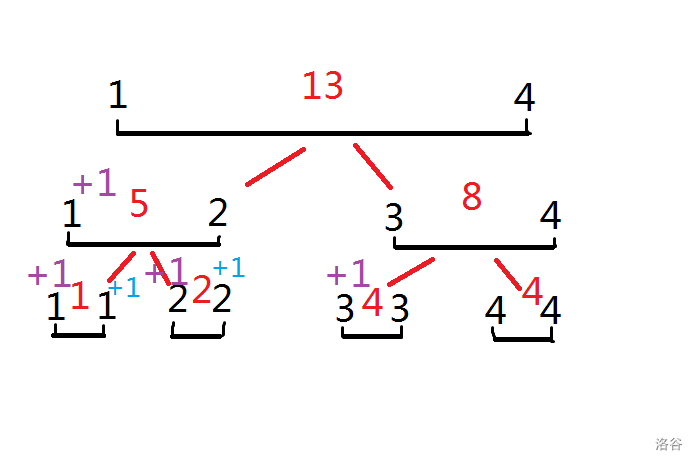
然后,我们怎么修改这个区间的单点,其实这个相对简单很多,你要把区间的第 dis 位加上 $k$。
那么你从根节点开始,看这个 dis 是在左儿子还是在右儿子,在哪往哪跑,
然后返回的时候,还是按照 tree[i].sum=tree[i*2].sum+tree[i*2+1].sum 的原则,更新所有路过的点。
如果不理解,我还是画个图吧,其中紫色是去的路径,粉色是返回的路径,回来时候红色的+标记就是把这个点加上这个值。
把这个过程变成代码,就是这个样子:1
2
3
4
5
6
7
8
9
10inline void add(int i,int dis,int k){
if(tree[i].l==tree[i].r){//如果是叶子节点,那么说明找到了
tree[i].sum+=k;
return ;
}
if(dis<=tree[i*2].r) add(i*2,dis,k);//在哪往哪跑
else add(i*2+1,dis,k);
tree[i].sum=tree[i*2].sum+tree[i*2+1].sum;//返回更新
return ;
}
2.2$\quad$区间修改,单点查询
区间修改和单点查询,我们的思路就变为:如果把这个区间加上 $k$,相当于把这个区间涂上一个 $k$ 的标记,然后单点查询的时候,就从上跑道下,把沿路的标记加起来就好。
这里面给区间贴标记的方式与上面的区间查找类似,原则还是那三条,只不过第一条:如果这个区间被完全包括在目标区间里面,直接返回这个区间的值变为了如果这个区间如果这个区间被完全包括在目标区间里面,讲这个区间标记 $k$。
具体做法很像,这里贴上代码:1
2
3
4
5
6
7
8
9
10inline void add(int i,int l,int r,int k){
if(tree[i].l>=l && tree[i].r<=r){//如果这个区间被完全包括在目标区间里面,讲这个区间标记k
tree[i].sum+=k;
return ;
}
if(tree[i*2].r>=l)
add(i*2,l,r,k);
if(tree[i*2+1].l<=r)
add(i*2+1,l,r,k);
}
然后就是单点查询了,这个更好理解了,就是 dis 在哪往哪跑,把路径上所有的标价加上就好了:1
2
3
4
5
6
7
8
9void search(int i,int dis){
ans+=tree[i].num;//一路加起来
if(tree[i].l==tree[i].r)
return ;
if(dis<=tree[i*2].r)
search(i*2,dis);
if(dis>=tree[i*2+1].l)
search(i*2+1,dis);
}
不知不觉,这第二章已经结束。这样的简单(原谅我用这个词)线段树,还可除了求和,还可以求区间最小最大值,还可以区间染色。
但是!这样的线段树展现不出来她的魅力,因为区间求和,树状数组比她少了一个很大的常熟。二区间最值,ST的那神乎其技的$O(n)$查询也能完爆她。这是为什么?因为线段树的魅力还没有展现出来,她最美丽的地方:$\text{pushdown}$ 还未展现于世,如果你已经对这一章充足的了解,并且能不看博客把洛谷上树状数组模板1、2都能写出来,那么请你进入下一部。
三、进阶线段树
区间修改、区间查询,你可能会认为,把上一章里面的这两个模块加在一起就好了,然后你就会发现你大错特错。
因为如果对于1~4这个区间,你把1~3区间+1,相当于把节点1~2和3标记,但是如果你查询2~4时,你会发现你加的时没有标记的2节点和没有标记的3~4节点加上去,结果当然是错的。
那么我们应该怎么办?这时候 $\text{pushdown}$ 的作用就显现出来了。
你会想到,我们只需要在查询的时候,如果我们要查的2节点在1~2区间的里面,那我们就可以把1~2区间标记的那个+1给推下去这样就能顺利地加上了。
怎么记录这个标记呢?我们需要记录一个“懒标记” $\text{lazytage}$,来记录这个区间
区间修改的时候,我们按照如下原则:
- 如果当前区间被完全覆盖在目标区间里,讲这个区间的
sum+k*(tree[i].r-tree[i].l+1) - 如果没有完全覆盖,则先下传懒标记
- 如果这个区间的左儿子和目标区间有交集,那么搜索左儿子
如果这个区间的右儿子和目标区间有交集,那么搜索右儿子
然后查询的时候,将这个懒标记下传就好了,下面图解一下:
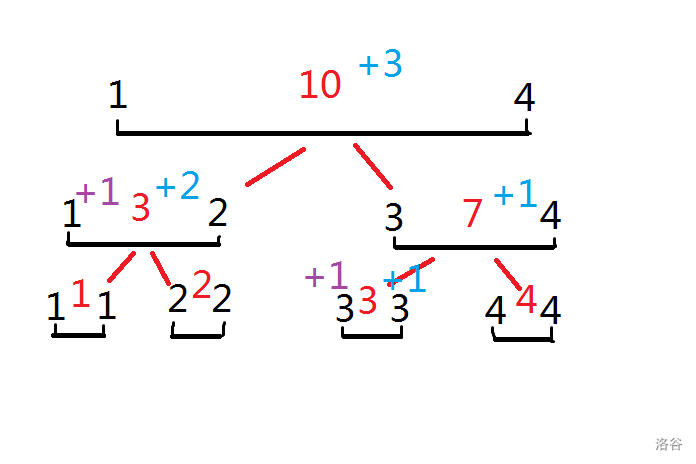
如图,区间1~4分别是1、2、3、4,我们要把1~3区间+1。因为1~2区间被完全覆盖,所以将其+2,并将紫色的 $\text{lazytage}+1$,3区间同理
注意我们处理完这些以后,还是要按照 tree[i].sum=tree[i*2].sum+tree[i*2+1].sum 的原则返回,代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16void add(int i,int l,int r,int k)
{
if(tree[i].r<=r && tree[i].l>=l)//如果当前区间被完全覆盖在目标区间里,讲这个区间的sum+k*(tree[i].r-tree[i].l+1)
{
tree[i].sum+=k*(tree[i].r-tree[i].l+1);
tree[i].lz+=k;//记录lazytage
return ;
}
push_down(i);//向下传递
if(tree[i*2].r>=l)
add(i*2,l,r,k);
if(tree[i*2+1].l<=r)
add(i*2+1,l,r,k);
tree[i].sum=tree[i*2].sum+tree[i*2+1].sum;
return ;
}
其中的 $\text{pushdown}$,就是把自己的 $\text{lazytage}$ 归零,并给自己的儿子加上,并让自己的儿子加上 $k\times(r-l+1)$
1 | void push_down(int i) |
查询的时候,和上一章的几乎一样,就是也要像修改一样加入 $\text{pushdown}$,这里用图模拟一下。我们要查询2~4区间的和,这是查询前的情况,所有紫色的代表 $\text{lazytage}$
然后,我们查到区间1~2时,发现这个区间并没有被完全包括在目标区间里,于是我们就 $\text{pushdown}$,$\text{lazytage}$ 下传,并让每个区间 sum 加上 $(r-l)\text{lazytage}$。
然后查到2~2区间,发现被完全包含,所以就返3,再搜索到3~4区间,发现被完全包含,那么直接返回8,最后3+8=11就是答案
这里是代码实现:
1 | inline int search(int i,int l,int r){ |
好了,到了这里,我们就学会了用线段树进行区间加减操作,大家可以完成洛谷的线段树模板1
四、乘法(根号)线段树
4.1$\quad$乘法线段树
如果这个线段树只有乘法,那么直接加入 $\text{lazytage}$ 变成乘,然后 tree[i].sum*=k 就好了。但是,如果我们是又加又乘,那就不一样了。
当 $\text{lazytage}$ 下标传递的时候,我们需要考虑,是先加再乘还是先乘再加。我们只需要对 $\text{lazytage}$ 做这样一个处理。
$\text{lazytage}$分为两种,分别是加法的 plz 和乘法的 mlz。
$mlz$很简单处理,$pushdown$时直接$\times$父亲的就可以了,那么加法呢?
我们需要把原先的 plz 乘上父亲的 mlz 再加上父亲的 plz。1
2
3
4
5
6
7
8
9
10
11
12inline void pushdown(long long i){//注意这种级别的数据一定要开long long
long long k1=tree[i].mlz,k2=tree[i].plz;
tree[i<<1].sum=(tree[i<<1].sum*k1+k2*(tree[i<<1].r-tree[i<<1].l+1))%p;//
tree[i<<1|1].sum=(tree[i<<1|1].sum*k1+k2*(tree[i<<1|1].r-tree[i<<1|1].l+1))%p;
tree[i<<1].mlz=(tree[i<<1].mlz*k1)%p;
tree[i<<1|1].mlz=(tree[i<<1|1].mlz*k1)%p;
tree[i<<1].plz=(tree[i<<1].plz*k1+k2)%p;
tree[i<<1|1].plz=(tree[i<<1|1].plz*k1+k2)%p;
tree[i].plz=0;
tree[i].mlz=1;
return ;
}
然后加法和减法的函数同理,维护 $\text{lazytage}$ 的时候加法标记一定要记得现乘再加。
值得一提的是,计算$\times$2时一定要改成 $i<<1$ 这样能解决很多时间。
4.2$\quad$根号线段树
其实,根号线段树和除法线段树一样。她们乍眼一看感觉直接用 lazytage 标记除了多少,但是实际上,会出现精度问题。
C++的除法是向下取整,很明显,$\dfrac{a+b}{k}!=\dfrac{a}{k}+\dfrac{b}{k}$(在向下取整的情况下),而根号,很明显$\sqrt{a}+\sqrt{b}!=\sqrt{a+b}$ 那么怎么办?
第一个想法就是暴力,对于每个要改动的区间l~r,把里面的每个点都单独除,但这样就会把时间复杂度卡得比大暴力都慢(因为多个常数),所以怎么优化?
我们对于每个区间,维护她的最大值和最小值,然后每次修改时,如果这个区间的最大值根号和最小值的根号一样,说明这个区间整体根号不会产生误差,就直接修改(除法同理)
其中, lazytage 把除法当成减法,记录的是这个区间里每个元素减去的值。
下面是根号线段树的修改过程:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19inline void Sqrt(int i,int l,int r){
if(tree[i].l>=l && tree[i].r<=r && (tree[i].minn-(long long)sqrt(tree[i].minn))==(tree[i].maxx-(long long)sqrt(tree[i].maxx))){//如果这个区间的最大值最小值一样
long long u=tree[i].minn-(long long)sqrt(tree[i].minn);//计算区间中每个元素需要减去的
tree[i].lz+=u;
tree[i].sum-=(tree[i].r-tree[i].l+1)*u;
tree[i].minn-=u;
tree[i].maxx-=u;
return ;
}
if(tree[i].r<l || tree[i].l>r) return ;
push_down(i);
if(tree[i*2].r>=l) Sqrt(i*2,l,r);
if(tree[i*2+1].l<=r) Sqrt(i*2+1,l,r);
tree[i].sum=tree[i*2].sum+tree[i*2+1].sum;
tree[i].minn=min(tree[i*2].minn,tree[i*2+1].minn);//维护最大值和最小值
tree[i].maxx=max(tree[i*2].maxx,tree[i*2+1].maxx);
//cout<<"i"<<i<<" "<<tree[i].sum<<endl;
return ;
}
然后 pushdown 没什么变化,就是要记得 tree[i].minn$、$tree[i].maxx 也要记得 -lazytage。